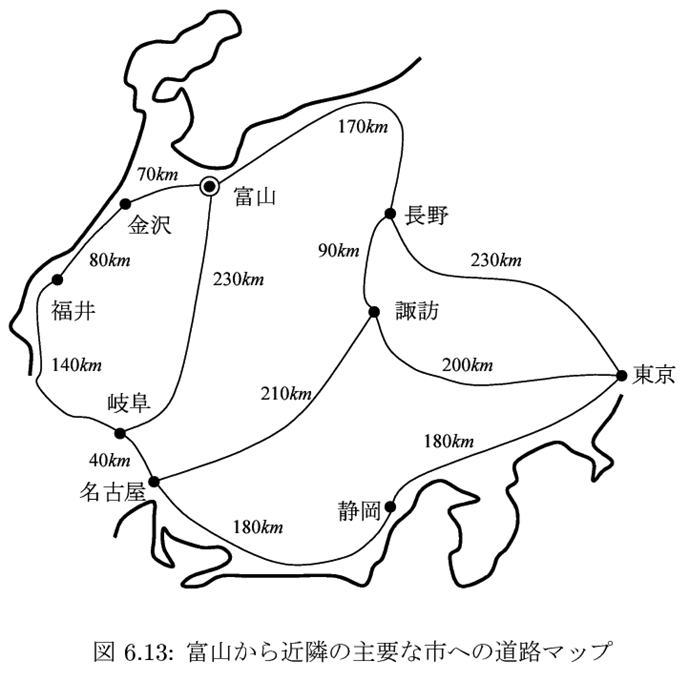
<問題>
gcc -c 0605.c
gcc -o 0605 0605.obj list1.obj

頂点番号は、以下 1 2 3 4 5 6 7 8 9 富山、金沢、福井、長野、岐阜、諏訪、名古屋、静岡、東京
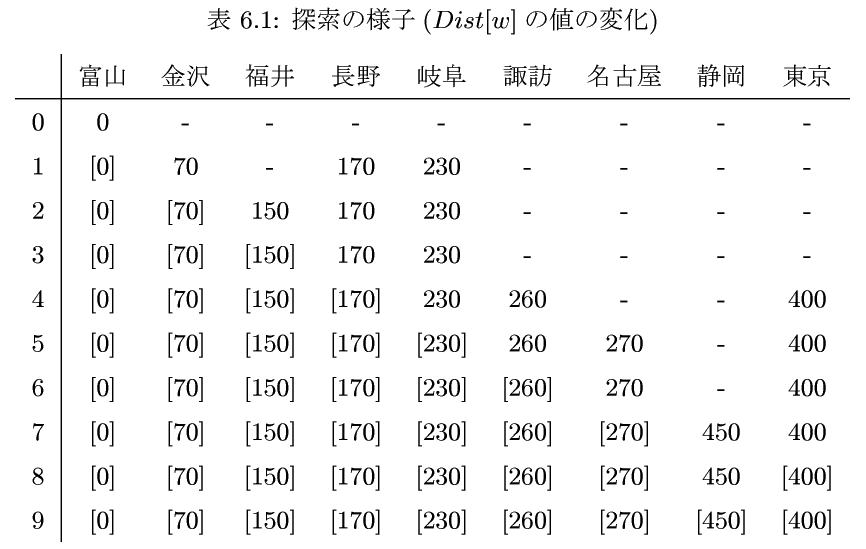
<実行結果 例> vertex1 to 2: dist:70 to 4: dist:170 to 5: dist:230 vertex2 to 1: dist:70 to 3: dist:80 vertex3 to 2: dist:80 to 5: dist:140 vertex4 to 1: dist:170 to 6: dist:90 to 9: dist:230 vertex5 to 1: dist:230 to 3: dist:140 to 7: dist:40 vertex6 to 4: dist:90 to 7: dist:210 to 9: dist:200 vertex7 to 5: dist:40 to 6: dist:210 to 8: dist:180 vertex8 to 7: dist:180 to 9: dist:180 vertex9 to 4: dist:230 to 6: dist:200 to 8: dist:180 1 -> 1 : 0 1 1 -> 2 : 70 1 2 1 -> 3 : 150 1 2 3 1 -> 4 : 170 1 4 1 -> 5 : 230 1 5 1 -> 6 : 260 1 4 6 1 -> 7 : 270 1 5 7 1 -> 9 : 400 1 4 9 1 -> 8 : 450 1 5 7 8
#include "list1.h"
#define N 9
List *Out[N+1]; /* 配列の各要素はList 個数は0から始まらないのでN+1にする*/
int less(int a, int b);
int exist(List *n, int u);
void Dijkstra(int v);
/* 小さい値を戻り値 */
int less(int a, int b){
if(a < b){
return(a);
} else {
return(b);
}
}
/* 探索リストn に含まれる頂点かどうかを判定 */
int exist(List *n, int u){
List *w;
for (w = n->next; w != NULL; w = w->next) {
if (u == w->data){
return(1);
}
}
return(0);
}
void Dijkstra(int v0){
int m, v, i, j, in[N+1]; /* 各頂点の1つ前(なのでin。出るものはout) */
int visit[N+1], dist[N+1]; /* 各配列頂点nについて、確定済情報、最短距離 */
List *n, *w, *u, *s, *route[N+1];
/* nは探索中リスト wは探索リスト操作用ポインター
uは隣接OUTリスト操作用ポインター routeは、各頂点んへの経路リスト */
for(i = 0 ; i < N+1; i++) {
visit[i] = 0; /* 最短距離確定情報リスト、全ての頂点を0に */
route[i] = create(); /* 経路情報。まずはヌル */
}
n=create();
insert(n, 1, v0, 0); /* n の先頭には、スタート頂点 */
dist[v0] = 0;
in[v0] = v0; /* スタートのみ、自分自身で初期化 */
while (!empty(n)) { /* 教科書ではempty_l 探索リストがなくなるまで */
m = 9999; /* 比較のため、ありえない値を暫定最小距離にする */
i = 1;
/* 現状のnについて、距離が最小の頂点を求める */
for (w = n->next; w != NULL; w = w->next) {
if (m > dist[w->data]) { /* 頂点までの距離がmより小さいなら */
m = dist[w->data]; /* 暫定最小値 mを更新 */
v = w->data; /* 暫定最短頂点vを更新 */
/* u = w; */ /* 作者のミス。いらない */
j=i; /* この情報のnリストの位置を記録 */
}
i++; /* リスト内の位置カウンター */
}
/* 確定した最小値について */
visit[v] = 1; /* visit配列に、確定を記録 */
delete(n,j); /* 探索リストnから、j番目の頂点をdelete */
printf("%d -> %d : %d\n", v0, v, dist[v]); /* 確定情報のプリント */
s = route[v]; /* 決定したvの経路リスト先頭アドレス */
/* 一つ前の頂点までの経路をコピー */
for (w = route[in[v]] -> next; w != NULL; w = w->next) {
insert(s, 1, w->data, 0); /* 経路なので、distメンバーは0に */
s = s->next; /* スタックでもよいが、ここではリスト(キュー)を使用 */
}
insert(s, 1, v, 0); /* 一番最後に自分自身 */
printlist1(route[v]); /* 経路の出力 printlist1は、list1.cで定義 */
/* このプログラムの最後にprintlist1を置きます */
/* 確定した頂点vから、ひとつ先の頂点の情報で、全体情報を更新 */
for (u = Out[v]->next; u != NULL; u = u->next) {
if (visit[u->data] == 0){ /* 未確定の頂点の場合 */
if (exist(n, u->data)) { /* 探索リストnにある頂点の場合 */
if (dist[v]+u->dist < dist[u->data]) /* vを経由した方が短い */
in[u->data] = v; /* 1つ前をvに更新 */
/* より短い距離で、更新 */
dist[u->data] = less(dist[u->data], dist[v]+u->dist);
} else {
/* 探索リストにない頂点の場合は、追加。
また、vまでの距離+隣接距離を登録 */
insert(n,1,u->data,0);
in[u->data] = v; /* 1つ前 */
dist[u->data] = dist[v]+u->dist;
} /* if else 文 */
} /* if 文 */
} /* for ループ end */
} /* while ループ end */
free(n); /* nリストをフリー */
}
int main(void){
int i;
/* 頂点のidを1からとするので、i=0は使用しない */
for(i=1;i<N+1;i++){
Out[i]=create();
}
/* 1 2 3 4 5 6 7 8 9 */
/* 富山 金沢 福井 長野 岐阜 諏訪 名古屋 静岡 東京 */
/* 隣接リスト(重み;距離つき)を、リスト構造に格納 */
/* 図6.13 各都市のデータ */
insert(Out[1],1,2,70); insert(Out[1],2,4,170); insert(Out[1], 3, 5, 230);
insert(Out[2],1,1,70); insert(Out[2],2,3,80);
insert(Out[3],1,2,80); insert(Out[3],2,5,140);
insert(Out[4],1,1,170); insert(Out[4],2,6,90); insert(Out[4],3,9,230);
insert(Out[5],1,1,230); insert(Out[5],2,3,140);insert(Out[5],3,7,40);
insert(Out[6],1,4,90); insert(Out[6],2,7,210); insert(Out[6],3,9,200);
insert(Out[7],1,5,40); insert(Out[7],2,6,210); insert(Out[7],3,8,180);
insert(Out[8],1,7,180); insert(Out[8],2,9,180);
insert(Out[9],1,4,230); insert(Out[9],2,6,200);insert(Out[9],3,8,180);
/* 各頂点について、隣接リストの表示 */
for(i=1; i<N+1; i++){
printf("vertex%d\n", i);
printlist(Out[i]);
}
/* ダイクストラ法で、頂点1から、最短距離を求めよ*/
Dijkstra(1);
/* Freeするなら */
for(i=1; i<N+1; i++){
FreeData(Out[i]);
}
return(0);
}
/* 経路をプリントするために */
void printlist1 (List *L) {
while (L != NULL) {
if (L -> data != -1) /* ありえない-1だったら、ダミー。プリントしない */
printf(" %d ", L -> data);
L = L -> next;
}
printf("\n");
}