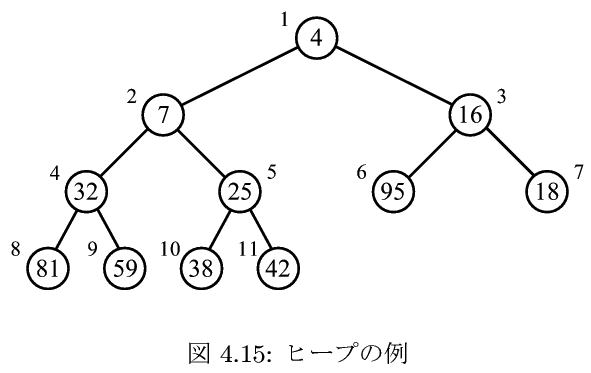
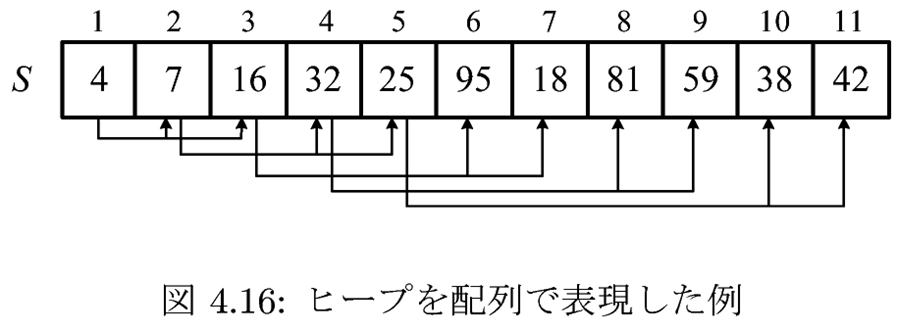
図4.15のヒープを、図4.16のように配列に表現する。(教科書の実行例とプログラムの実行例の対応をとりやすくするために、S[0]は使わず、1つ目の要素はS[1]からとする。プログラムに注意)

<問題>
ヒープソート (p.95 演習問題4.4 ヒープソート)
<実行例> 毎回の交換結果のヒープの内容をプリントしている。(この実行例でなくてもよい)
1 2 3 4 5 6 7 8 9 10 11 4 7 16 32 25 95 18 81 59 38 42 (mainループからの呼び出し。delete_min前) 4 (ヒープを階層ごとにプリントしたもの) 7 16 32 25 95 18 81 59 38 42 1 2 3 4 5 6 7 8 9 10 (down_heap中の交換 2の7は、1へ) 7 7 16 32 25 95 18 81 59 38 1 2 3 4 5 6 7 8 9 10 (5の25は、2へ) 7 25 16 32 25 95 18 81 59 38 1 2 3 4 5 6 7 8 9 10 (10の38は、5へ) 7 25 16 32 38 95 18 81 59 38 1 2 3 4 5 6 7 8 9 10 7 25 16 32 38 95 18 81 59 42 (mainループからの呼び出し。delete_min(再構成)後 42は、10へ) 7 25 16 32 38 95 18 81 59 42 (ヒープを階層ごとにプリントしたもの)
解答例
#include <stdio.h>
#define N 11 /* 要素は11 */
void down_heap(int k, int r);
void delete_min(void);
void print_heap(int n);
void printtree_heap(int n);
/* S[0]は、使用しない。0を入れておく */
/* 11個の要素にS[11]まで用意するには、S[11+1] */
int S[N+1]={0,4,7,16,32,25,95,18,81,59,38,42};
void print_heap(int n) {
int i;
/* 要素番号 */
for (i=1; i <= n; i++)
printf("%3d", i);
printf("\n");
/* 値 */
for (i=1; i <= n; i++)
printf("%3d",S[i]);
printf("\n");
printf("\n");
}
void print_tree_heap(int n){
int i, j;
/* 2の累乗ごとに改行 */
for (i = 1 ; i <= n; i = i*2) {
for (j= i ; (j < i*2 && j <= n) ; j++)
printf("%3d", S[j]);
printf("\n");
}
printf("\n\n");
}
void down_heap(int k, int r){
int i, j, v;
v=S[k]; /* 最上位の親の値 vは最後まで変わらないので注意 */
i=k; /* 親 i 一番最初は最上位 下ではiの位置にvがあってよいのかをチェック する */
j=2*k; /* 子 j */
while(1){
if(j < r && S[j] > S[j+1]) { /* 2つの子の比較。右の子の値が小さいとき */
j++; /* 右の子を親と比較するためにセット */
}
if(j <= r && v > S[j]) {
/* このiの位置にvをもってきたとしたら親の方が大きい。vはここより下でなければ */
S[i]=S[j]; /* そこで、子の値を親にもちあげる */
i=j; /* 子のインデックスを親のインデックスに */
j=2*j; /* その親の子へ。これら2つの操作が、下へ向かっていることに 対応 */
print_heap(N-1); /* ヒープの状況をプリントする */
} else {
break; /* vが子より小さい。このiの位置にvがあるべきだ。whileループを飛び出す */
}
}
S[i]=v; /* ここで最上位の親の値を最後に代入 */
}
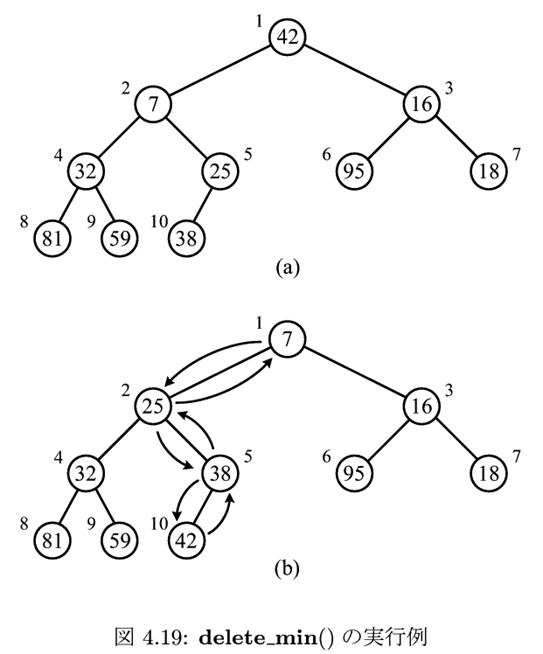
void delete_min(void) {
static int n=N;
S[1]=S[n]; /* 最後尾の要素を、ルートに */
n--; /* ヒープ要素数をデクリメント */
down_heap(1,n); /* 1-nのヒープを、下方に再構成。*/
}
int main(void){
int i;
print_heap(N); /* ヒープの配列をプリント */
print_tree_heap(N); /* ヒープを階層にプリント */
delete_min(); /* 最小値 (つまり、ルート)を削除し、再構成 */
print_heap(N-1);
print_tree_heap(N-1);
return(0);
}