中京大学工学部機械システム工学科 沼田宗敏 研究室 人型サッカーロボットと表面粗さ用フィルタの研究をする Numada Laboratory
研究内容
研究紹介
![]() 【重点研究:粗さ用フィルタ】
【重点研究:粗さ用フィルタ】
![]() 【人 工 知 能】
【人 工 知 能】
![]() 【コンピュータビジョン】
【コンピュータビジョン】
![]() 【ロボットサッカー】
【ロボットサッカー】
重要研究:粗さ用フィルタ
■解説論文:プラトーホーニング面などの機能性表面に有効なロバストフィルタの動向と事例

砥粒加工学会誌,Vol.61, No.11, pp.590-593 (2017.11)
図 フィルタ処理前のプラトー面
本解説論文では、測定データから表面粗さの評価まで、プラトーホーニング面のような特殊な表面も
含めてデジタルフィルタを中心に紹介している。
■JIS B 0634(2017年7月制定)で本研究室論文2報が引用される
2017年7月、JIS B 0634(製品の幾何特性(GPS)-フィルタ処理-線形の輪郭曲線フィルタ:ガ ウシアンフィルタ)が制定されました。これは2011年に発行されたISO 16610-21を基に作成された日 本工業規格です。これに伴いJIS B 0632(2001年)は廃止され、この規格に置き換えられました。この JIS B 0632の改訂およびJISのISOの流れについては以下のリンクを参照下さい。
JISのISO化の流れ(2016年1月14日中部経済新聞掲載)
なおJIS B 0634の解説では、当研究室の下記2報の論文が引用されています。
・沼田宗敏,野村俊,神谷和秀,田代発造,輿水大和:
有限長データ用ローパスフィルタの研究(第2報)-最小2乗基準によるローパスフィルタ-,
精密工学会誌, Vol. 72, No. 5, pp. 607-611, (2006. 5).
・近藤雄基,沼田宗敏,輿水大和,神谷和秀,吉田一朗:
ロバスト性調整可能な高速M推定ガウシアンフィルタ,
精密工学会誌, Vol. 82, No. 3 272-277 (2016.3).
■ 英文論文:振幅伝達特性を保持したエンド効果のないローパスフィルタ

Precision Engineering, Vol.48, pp.243-253 (Apr. 2017)
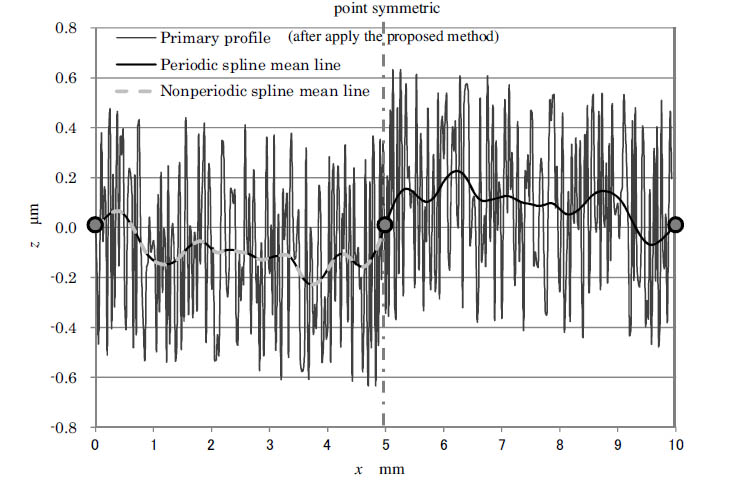
図 点対称拡張により周期スプラインと非周期スプラインの出力が一致
点対称拡張法によりローパスフィルタのエンド効果をなくし、振幅伝達特性が保持される手法を示し
た。点対称拡張により周期性をもたせた元データのエンド効果が解消され、これにより本来のローパス
フィルタの振幅伝達率が得られる。
たとえば、エンド効果に有効なスプラインフィルタは非周期スプラインであるが、よく知られたスプラ
インフィルタの振幅伝達特性は周期スプラインである。通常は出力も振幅伝達率も一致しない。これ
を本提案手法を用いると、周期スプラインを用いたスプラインフィルタの出力と非周期スプラインを用
いたスプラインフィルタの出力が一致するようになる。このため、非周期スプラインフィルタの振幅伝
達率もよく知られたスプラインフィルタの振幅伝達率として求めることができる。
■ 英文論文:実データを用いたローパスフィルタの振幅伝達特性の計算手法

Precision Engineering, Vol.44, pp.55-61 (Apr. 2016)
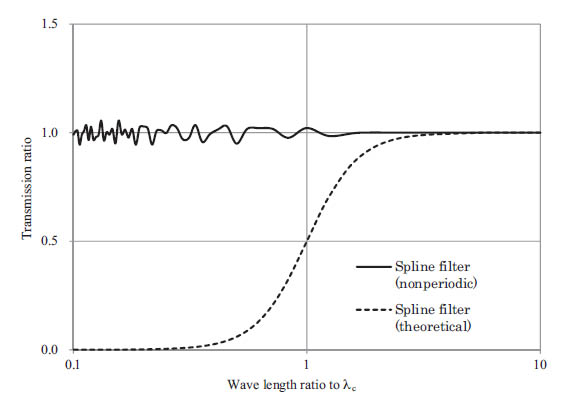
図 スプラインフィルタの理論的振幅伝達率と実際の振幅伝達率は異なる。
表面粗さ測定の現場で使われるローパスフィルタは、ISOのデータシートに記された振幅伝達率を持
っていると皆思っている。エンド効果の影響のないスプラインフィルタ、外れ値の影響を受けないロバ
ストガウシアンフィルタ、これらの振幅伝達率はスプラインフィルタの振幅伝達率、ガウシアンフィル
タの振幅伝達率に一致するかほぼ一致するものと期待されるが、普通に計算すると全く異なる結果が得
られる。本研究では正しい振幅伝達率の計算方法を提示する。
■招待講演「究極のフィルタ演算と普及策」(2016年3月 於ホテルニューオータニ長岡)

2016年3月、ホテルニューオータニ長岡で、表面性状分野の第一人者である長岡技術科学大学 柳 和久
教授の定年退職記念シンポジウムが第3回「にいがたナノ基盤技術実践会」講演会として開催された。
沼田教授は「究極のフィルタ演算と普及策」と題して、高速M推定を用いたロバストガウシアンフィ
ルタについて講演した。これは、外れ値のないほとんどのデータに対してガウシアンフィルタと同じ出
力を与え、外れ値に対してはロバストにふるまうフィルタである。従来のロバストガウシアンフィルタ
がガウシアンフィルタの出力と異なる問題に対する究極の解決策が示された。
(詳細はこちら)
■高速M推定型ロバストガウシアンフィルタ(FMGF)
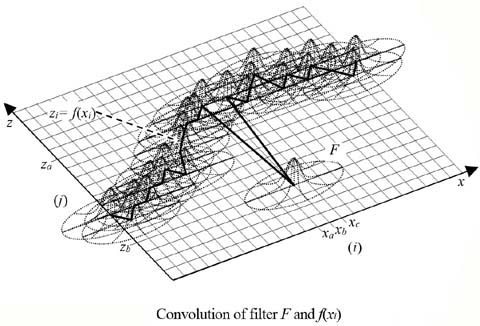
図 FMGFの概念図
高速M推定型ロバストガウシアンフィルタ(FMGF)は、ロバストな高速ガウシアンフィルタです。
データzi=f(xi)をxz座標系に展開した後、x方向にガウシアンフィルタ、z方向に2次Bスプラインフィル
タを適用、各xi座標上の最大点をフィルタ出力値として求めます。フィルタ出力値は2次Bスプライン曲
線の最大値として、解析的かつ高精度に計算できます。
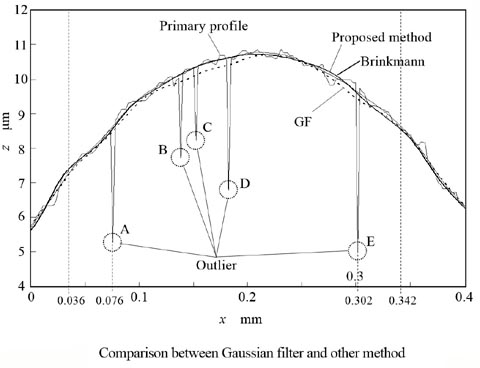
図 FMGFの処理例
高速M推定型ロバストガウシアンフィルタ(FMGF)は、外れ値のないデータに対しては業界標準の
ガウシアンフィルタと同一の結果を与え、外れ値がある場合にはロバストにふるまう理想的なフィルタ
です。2014年秋より本フィルタは、株式会社小坂研究所の表面粗さ測定機に搭載されています。
(論文)沼田宗敏,藤原孝幸,舟橋琢磨,輿水大和,神谷和秀,野村俊:高速M推定を用いたロバスト
ガウシアンフィルタの提案,精密工学会誌, Vol. 76, No.6, pp.684-688 (2010.6).
■高次M推定法
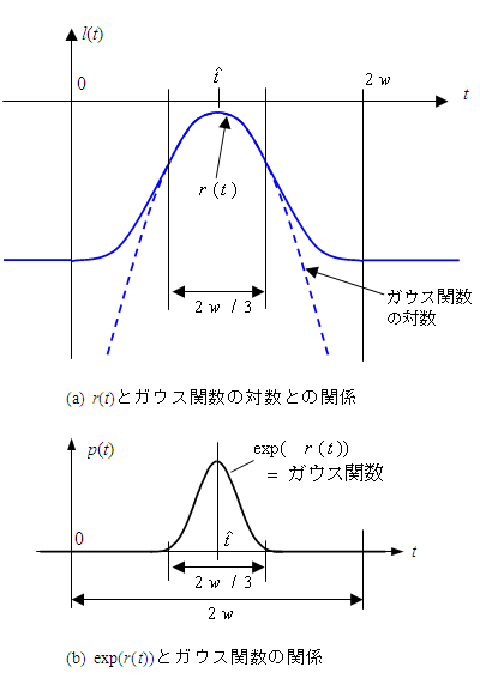
高速M推定関数 r(t)とガウス関数との関係
ガウス分布に従う観測値xiからある統計量tの最尤推定値を最尤推定で求めると、これは最小二乗法か
ら得られる結果に一致する。また,観測値に異常値が含まれる場合、最尤推定では推定値が異常値にひ
っぱられる。
これを解決するには、ロバスト推定の一手法であるM推定を用いるとよい。 しかし、M推定には以下
の問題が指摘されている。1つは推定値の誤差の二乗和を最小にする、M推定の基本式が繰り返し演算
でしか解けず、計算コストが極めて大きいことである。もう1つは、異常値が無い場合統計量の推定値
が、再尤推定値に一致しないことである。特に推定値を最尤推定値で与えるよう規格で定めている場合
には、推定関数がガウス関数の対数とは一致せず致命的となる。
提案する新しいM推定関数r(t)は、2次Bスプライン基底関数を拡大・平行移動したものである。
r(t)の幅をうまく選ぶことにより、観測値のほとんどで、推定関数とガウス関数の対数とが一致する。
このため、異常値のない観 測値に対しては、得られる推定値と最尤推定値とが一致する。また、推定値
は2次Bスプライン基底関数の線形和、すなわち2次Bスプライン曲線の最大点として解析的に計算で
きる。高速に計算可能なM推定であるため、これを高速M推定と呼んでいる。
(論文)沼田ら:「高速M推定を用いたロバストガウシアンフィルタの提案」
精密工学会誌 Vol.76,No.6,684-688,(2010).
■高次スプラインフィルタ
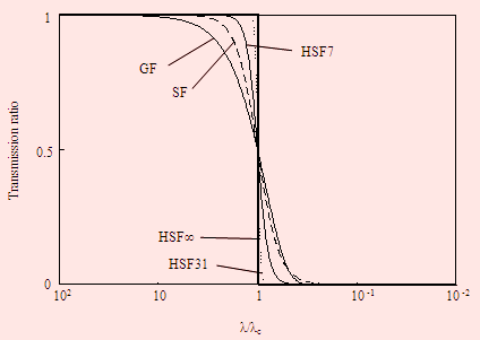
図 ガウシアンフィルタ・スプラインフィルタと
高次スプラインフィルタの振幅伝達特性比較
表面粗さ用平均値フィルタとして使われるガウシアンフィルタには、終端で予期せぬふるまいをする
エンドエフェクトとカットオフ特性がゆるやかな振幅伝達特性を持つという問題がある。本研究では、
最もなめらかな曲線である自然スプラインに注目し、それを用いた通常3次のスプラインフィルタの次
数を高次元化した。よりなめらかな曲線とするためである。これにより、カットオフ特性は次数の上昇
とともに急峻となり、無限次の高次スプラインフィルタのカットオフ特性はナイフエッジとなった。ま
た、高次スプラインフィルタの計算は逆行列を解かねばならず、次数増大とともに計算コストが増大す
る。この問題を、周波数領域にお ける計算で置き換えることにより解決し、また、エンドエフェクトの
問題も解決した。
(解説論文)加藤邦人,金子俊一,沼田宗敏: ロバスト画像処理の新展開, 精密工学会誌,
Vol. 75, No. 02, pp.237-245, (2009.02).
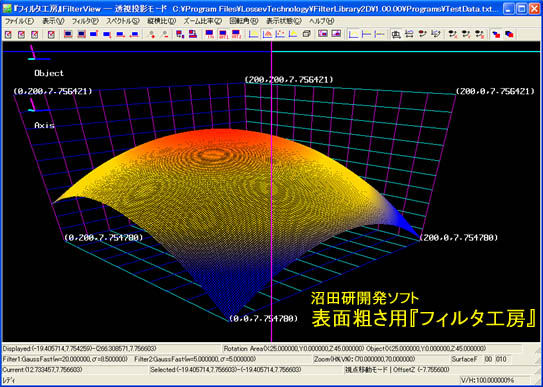
■高速2次元ガウシアンフィルタ
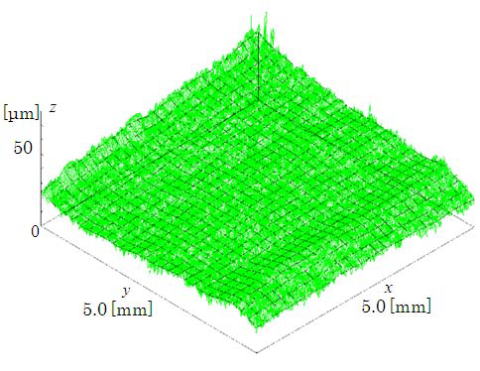
図 物体表面3次元形状と粗さ用平均値曲面
3次元表面粗さの測定における大きな問題は、計測点が膨大なため基準となる平均値曲面の算出に時
間を要することである。特に位相補償型ガウシアンフィルタを用いる場合には、この問題に加え、終端
で予期せぬ 結果が得られるエンド効果、xy方向と斜め方向のフィルタ特性が異なる方向特性への対応
も必要である。本研究では、ダウンサンプリングとGスプラインフィルタを用いた周波数領域法によっ
て、これらの問題を解決した高速2次元ガウシアンフィルタを提案している。
(論文)Munetoshi Numada, Takashi Nomura, Kazuhide Kamiya, Hatsuzo Tashiro and Hiroyasu Koshimizu: Filter with variable transmission characteristics for determination of three-dimensional roughness, Journal of the International Societies for Precision Engineering and Nanotechnology ※2, Vol. 30, No. 4, pp. 431-442, (Oct. 2006).
■周波数型自由曲面あてはめ
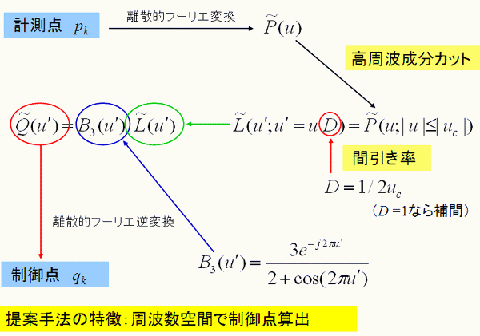
周波数型Bスプライン曲面あてはめ理論
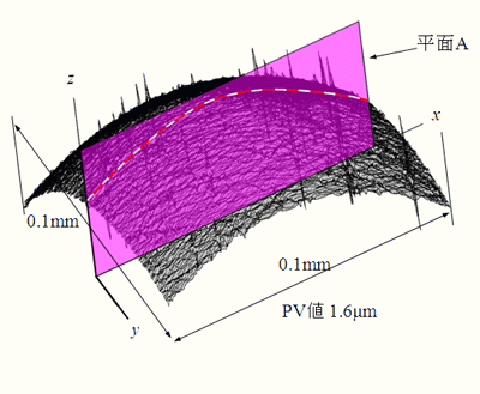
元データ
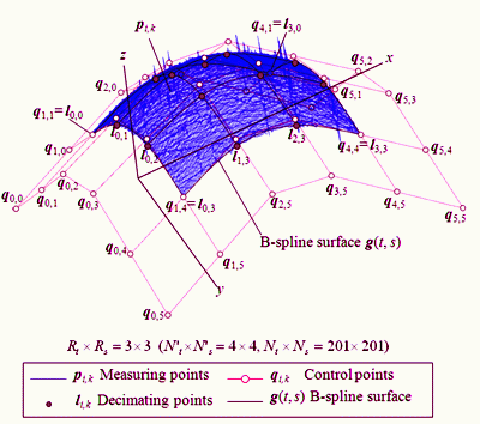
Bスプライン曲面の制御点
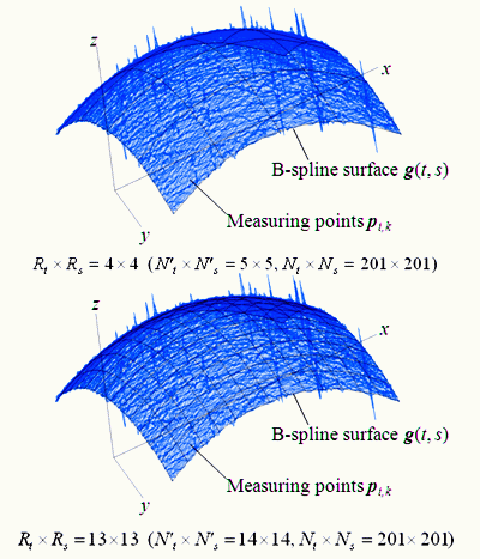
Bスプライン曲面あてはめ例(2例)
3次元座標で与えられた点群に自由曲面をあてはめることは容易ではない。最大の問題は計算コスト
である。この問題に対し、計測データを周波数空間へ変換した後にフィルタ処理し、実空間への逆変換
によって自由曲面の制御点を得る方法を提案した。提案手法では、Bスプライン曲面の終端における2
次微分が0になるように、計測データに対しある工夫が施される。これにより、従来の周波数型処理の
問題であった、終端でのリンギング発生がない。周波数空間におけるフィルタ処理は、実空間における
コンボルージョン処理に相当するため、大幅な高速処理が可能になった。なお、最も滑らかな補間関数
である「平滑化スプライン」によるあてはめも、提案手法を用いると高速に処理できる。
(論文)沼田ら:「高速離散的フーリエ変換を用いたB-spline曲面あてはめ」
精密工学会誌 Vol.71,No.7,860-867,(2005).
人工知能
・ディープラーニング(深層学習)
当研究室では2016年以来、ディープラーニング(深層学習)を用いた画像識別や、ロボット制御に取り組んでいます。
①AIステーション
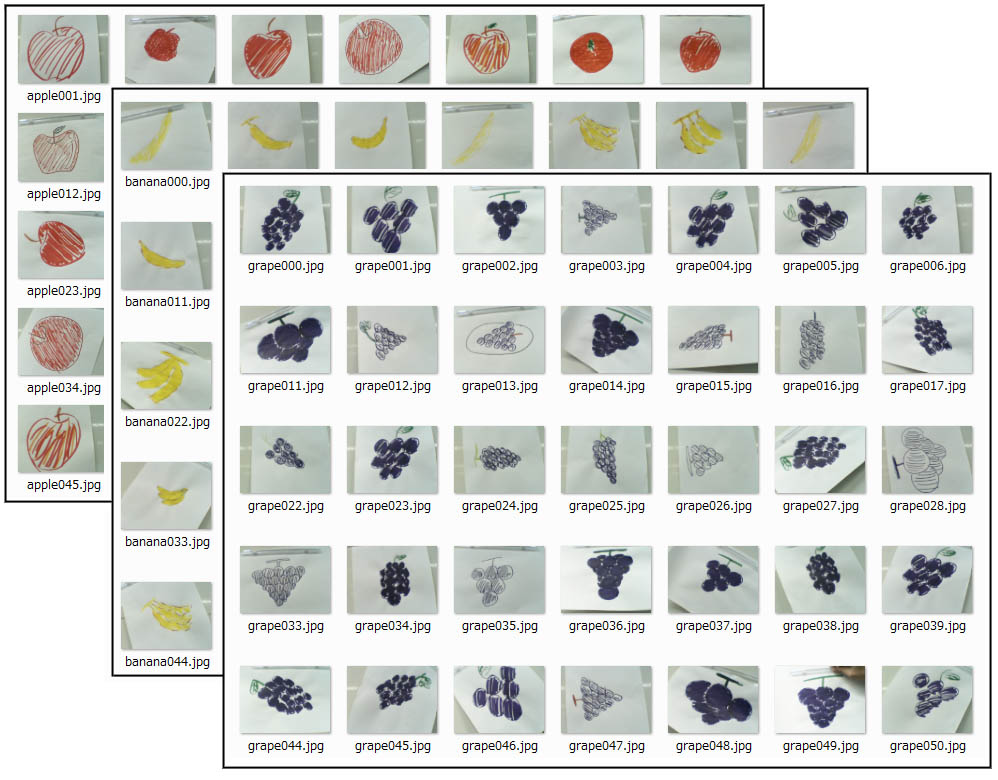
AI体験型マシンです。予め大量の画像データを学習させておくことにより、TVカメラで撮影された画像をディープラーニングにより識別します。
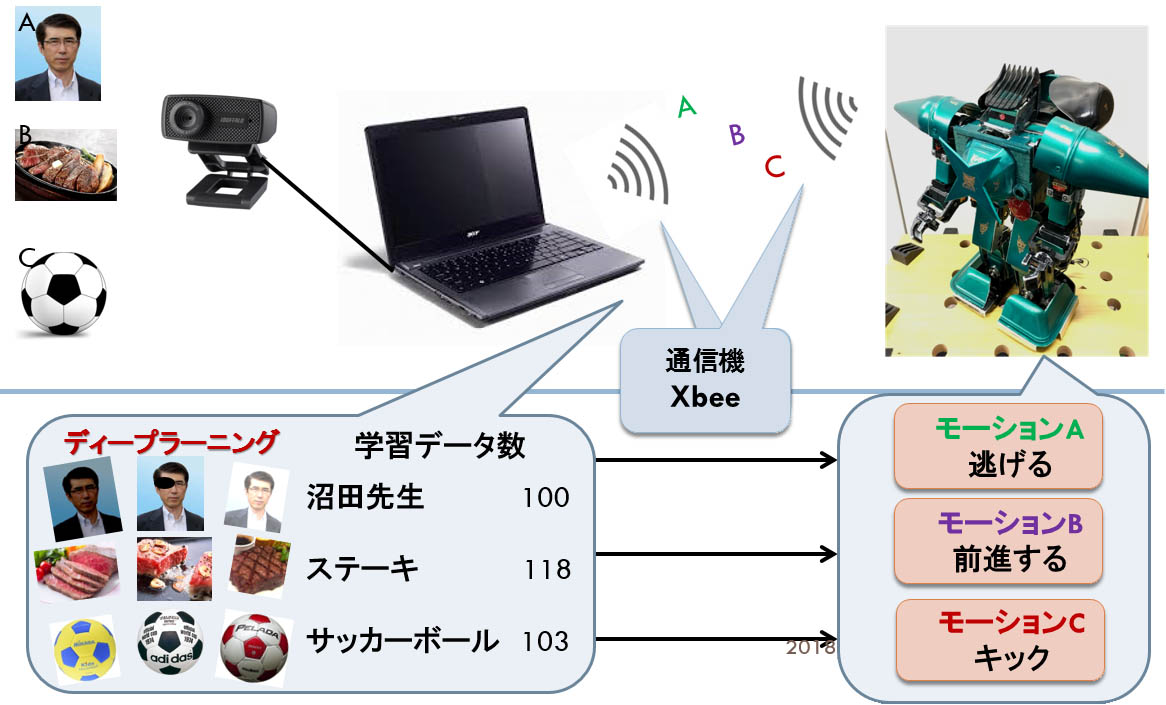
②ディープラーニングを用いたロボット動作
複数の対象物画像を予め大量に学習させておき、ディープラーニングにより対象物を識別すると、ロボットが自律的に動作します。
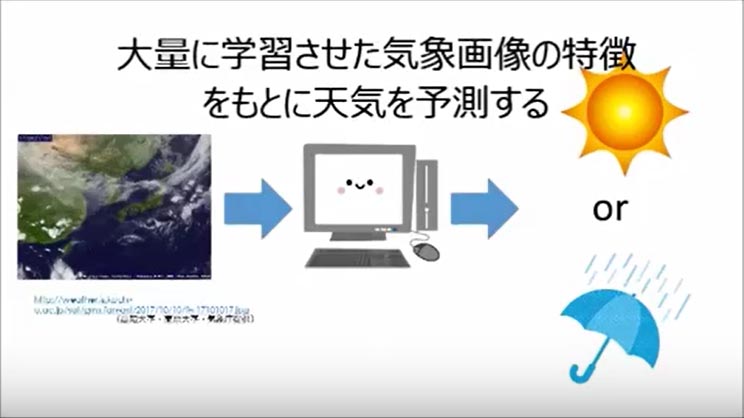
③ディープラーニングによる天気予測
20年間の気象衛星画像10000枚分をディープラーニングにより学習させ、翌日の天気(2016年名古屋市)を予測した。正解率は80%であった。
・マハラノビス距離を用いた機械学習
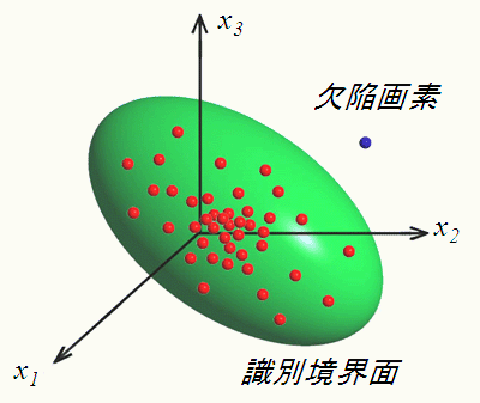
等確立密度点を形成する識別境界面
画像全体にn階層の平均処理を行い、これを1画素単位でみたときのn次元特 徴空間を定義する。続いて、この特徴空間を用いて良品サンプル画像を複数 枚学習させる。最後に、検査対象画素のn次元特徴空間におけるマハラノビ ス距離を計算し、局所欠陥および対極欠陥を検出する。 たとえば、下図(a)の古い百円硬貨(S54年製)のキズ検出を、新しい百円硬 貨(H17年製)との相違点で求めようとすると、(d)のようにいたるところに相 違点が発生し、求めるキズは検出できない。摩耗の影響を受けるからである。 これに対し、提案手法ではS51年製からH17年製までの百円硬貨を用いて学習 を行った。平均処理はn=3階層とした。摩耗の影響を受けず、キズだけを検出できた。
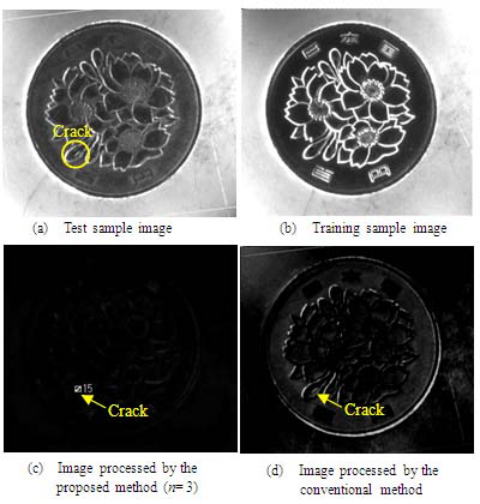
古い百円硬貨のキズ検出
(論文)沼田ら:「マハラノビス距離による学習を用いた大局的欠陥検査法」
精密工学会誌 Vol.75,No.2, 262-266,(ViEW推薦論文 2009).
コンピュータービジョン
・シーン認識(清水研と共同研究)
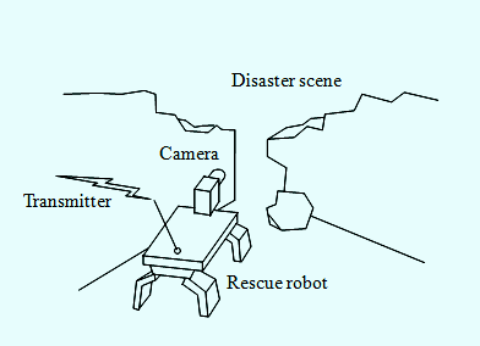
レスキューロボットのシーン認識

ルートを探索するレスキューロボット

認識されたシーンの稜線エッジ
巡航速度200mm/sで移動するレスキューロボットは、1フレーム33msの2-3倍の時間でシーン解析を行わなければならない。特に倒壊物や瓦礫の多い被災現
場用に、シーンのエッジ点群から高速に直線を検出する手法が望まれている。 本研究では、三項漸化式を用いた高速Hough変換法をシフト演算を用いてさら
なる高速化を図ることで、1フレームあたり10ms以内で処理を行う。
・ロバストなHough変換
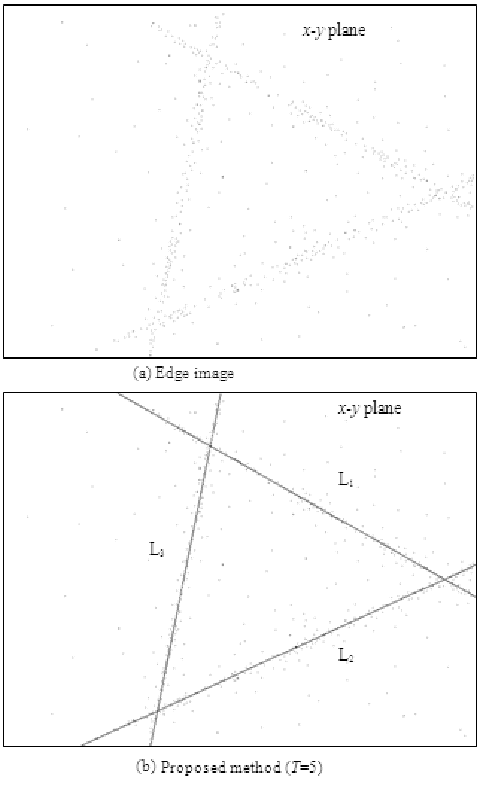
ばらつきのある点群からの直線検出
直線検出の有力な手法にHough変換があるが、ばらつきの大きい点群には適 用できない。ロバスト推
定の一手法であるLMedS法を用いたHough変換をだと、ばらつきが大きな点群からでも直線検出ができ
る。しかし、実時間での処理は不可能である。そこで、高速M推定を用いたHough変換を提案した。
LMedS法を用いたHough変換同様ばらつきの大きな点群からも直線検出が可能であるが、
処理時間は100倍以上早く、VGA画像に対し0.1秒台で処理できた。
(論文)沼田ら:「高速M推定を用いたロバストな高速Hough変換」
精密工学会誌 Vol.76,No.5,592-597,(2010).
ロボットサッカー

TV放映されたサッカーロボット ChukyoRoboStars(画面左)
(2013年5月7日「めざましテレビ」より (C)FUJI TELEVISION)
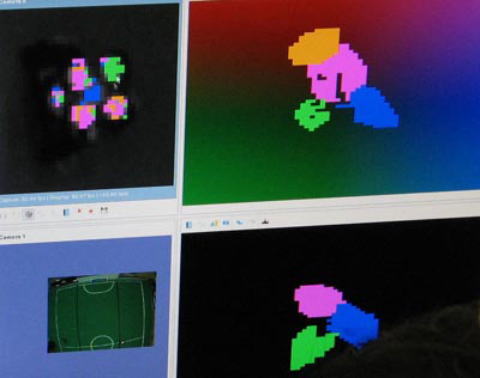
グローバルビジョン画像(SSLビジョン)
ロボット、人工知能、ビジョンという3つの技術の融合によって作られる自律サッカーロボット。
サッカーロボットによるサッカー競技では、試合中は一切ロボットやパソコンを操作することができま
せん。あらかじめ、ロボットに埋め込まれた戦略プログラムに基づき、味方、敵、ボールなどのカメラ
からの情報を刻一刻と認識しながら、最適のプレーを行います。

ロボカップ ジャパンオープン2019準決勝(Video)

ロボカップ ジャパンオープン2019決勝(Video)

ロボカップ ジャパンオープン2013(Video)
2010年5月の2010年5月のロボカップ・ジャパンオープンに初参戦のChukyo RoboStarsは、3年目
の2012年には初の決勝トーナメント進出を果たしました。そして、沼田ゼミ3年生(春見キャプテン)
によるロボットの根本的強化、人工知能プログラムの大幅見直しにより、2013年5月のロボカップ・ジャ
パンオープンではついに念願のベスト3に入りました。
2009年9月に立ち上げたばかりの研究室で、2010年5月のロボカップ・ジャ パンオープンに参加する
ことは無謀ともいえる挑戦でした。 しかし、幸いにも 大学から「プロジェクト型研究教育助成」を受
けて機器部品を揃えることができ、また輿水研院生のみなさんのプログラム作成へのご協力、そして何
よりも 沼田ゼミ1期生の学生たちの献身的なプログラム開発によって、何とか無事エントリーすること
ができました。もちろん、時間不足による調整・練習なしのいきなり本番出場であったため、サッカー
らしい動きをしたのはこのビデオのシー ンくらいでした。ともあれ、完全自律ロボットによるサッカー
試合:ロボカップという大きな舞台に第一歩を記すことができたことは大きな自信となりました。
中京大学 工学部 機械システム工学科
沼田宗敏研究室
〒466-8666
愛知県名古屋市昭和区八事本町101-2
TEL 052-835-7111(代)